Constructions de figures et calcul du périmètre A ) Construire un rectangle ABCD tel que AB = 10 cm et BC = 8 cm.
Tracer le point E, milieu de [AB].
Tracer le point F, milieu de [BC].
Tracer le point G, milieu de [CD].
Tracer le point H, milieu de [DA].
Tracer le point I, milieu de [AE].
Tracer le point J, milieu de [BF].
Tracer le point K, milieu de [CG].
Tracer le point L, milieu de [DH].
Construire le demi cercle de centre E et de rayon EI extérieur au rectangle.
Construire le demi cercle de centre F et de rayon FJ extérieur au rectangle.
Construire le demi cercle de centre G et de rayon GK extérieur au rectangle.
Construire le demi cercle de centre H et de rayon LH extérieur au rectangle.
Calculer le périmètre de la figure. En donner la valeur arrondie au mm près.
AI = IE = 2,5 cm
BJ= JF = 2 cm
La figure est formée d'un cercle de rayon FJ, d'un cercle de rayon IE, de 4 segments de longueur AI et de 4 segments de longueur BJ.
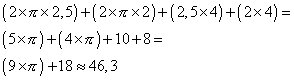
Le périmètre est égal à 46,3 cm environ.
BC = 10 cm ( à vérifier )
Tracer le milieu E de [BC].
Tracer le demi cercle de centre E et de rayon EB extérieur au triangle.
Calculer le périmètre de la figure. En donner la valeur arrondie au mm près.
le rayon du demi cercle est 5 cm
Le périmètre de la figure est environ 29,7 cm.
Tracer sur [AB] deux points E et F tels que AE = BF =
AB.Partager de la même façon les autres côtés en trois parties égales.
Tracer le demi cercle de diamètre EF extérieur au carré.
Tracer le quart de cercle de centre A et de rayon AE intérieur au carré.
Faire de même aux quatre sommets du carré.
Calculer le périmètre de la figure formée par les arcs de cercle. En donner la valeur arrondie au mm près.
EF = 4cm.
La figure est formée de deux cercles de rayon 2 cm ( à l'extérieur du carré) et d'un cercle ( à l'intérieur du carré) de rayon 4 cm.
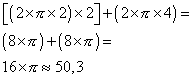
Le périmètre de la figure formée par les arcs de cercle est 50,3 cm environ.
Calculer le périmètre de la « fleur » formée par les arcs de cercle. En donner la valeur arrondie au mm près.
Pour construire la rosace, le cercle est partagé en six parties égales. Chaque branche de la rosace a donc une longueur égale au sixième de la longueur du cercle. La rosace est formée de 12 branches. Sa longueur est donc égale à deux fois celle du cercle de rayon 4 cm.
Le périmètre de la fleur est d'environ 50,3 cm.